The cross-section of the Møller scattering
![]() depends on the beam and target polarizations
depends on the beam and target polarizations
![]() and
and
![]() as:
as:
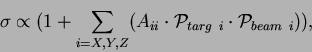 |
(B1) |
 |
(B2) |
The analyzing power does not depend on
the beam energy.
At
![]() the analyzing power has its maximum
the analyzing power has its maximum
![]() .
A transverse polarization also leads to an asymmetry, though the analyzing power is
lower:
.
A transverse polarization also leads to an asymmetry, though the analyzing power is
lower:
![]() . The main purpose of the polarimeter
is to measure the longitudinal component of the beam polarization.
. The main purpose of the polarimeter
is to measure the longitudinal component of the beam polarization.
The Møller polarimeter of Hall A detects pairs of scattered electrons in a
range of
![]() . The average analyzing power
is about
. The average analyzing power
is about ![]() .
.
The target consists of a thin magnetically saturated ferromagnetic foil.
In such a material about 2 electrons per atom can be
polarized. An average electron polarization of about 8% can be obtained.
In Hall A Møller polarimeter the foil is magnetized along its plane and
can be tilted at angles ![]() to the beam. The effective target
polarization is
to the beam. The effective target
polarization is
![]() .
.
The secondary electron pairs pass through a magnetic spectrometer which selects particles in a certain kinematic region. Two electrons are detected with a two-arm detector and the coincidence counting rate of the two arms is measured.
The beam longitudinal polarization is measured as:
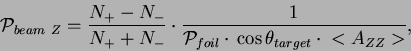 |
(B3) |
The target is rotated in the
horizontal plane. The beam polarization may have a horizontal
transverse component, which would interact with the horizontal transverse
component of the target polarization. The way to cancel the influence
of the transverse component is to take an average of the asymmetries
measured at 2 complimentary target angles, say 25 and ![]() .
.