SPD simulation page

UVa

The simulation for SPD timing and light yield is done as follows:
  1. Using SG crystal properties: rho=1.032g/cm3, n=1.58,
    1. BC404 (for CLAS12 TOF): attentuation length 140cm(bulk 160cm), rising time 0.7ns;
    2. BC408 (for SoLID): attenuation length 210cm (bulk 380cm), rising time should be 0.9ns but here I used 0.7ns by mistake;
  2. PMT specification as follows:
    1. QE: typically use 15%
    2. Timing:
      1. from these 3 references: CLAS note 91-003 (measured sigma with 200 photoelectrons); or Photonis catalog; or Hamamatsu website (datasheet):
      2. In Photonis catalog, open cathode TTS (listed in sigma) includes the center-edge difference, so the larger center-edge diff must be the full range (I think).

    		3.  CLAS note 91-003
      		catalog
      PMT
      		 rise time
      		 TTS
      		 rise time
      		 TTS
      Photonis XP2262
      		 3.0ns
      		 113ps*sqrt(200)=1.60ns
      		 2.0 or 2.3ns
      		 0.5ns sigma open cathode.
      (0.7ns center-edge difference)
      EMI 9954B05
      		 3.3ns
      		 101ps*sqrt(200)=1.43ns

      Burle 8575
      		 3.0ns
      		 144ps*sqrt(200)=2.04ns

      Hamamatsu R329
      		 4.0ns
      		 103ps*sqrt(200)=1.46ns
      		 2.6ns
      		 1.1ns (not sure if sigma or FWHM)
      XP2282B

      		1.5ns
      		 0.4ns sigma open cathode (that should include the center-edge difference);
      0.5ns center-edge difference (should this be the full variation then?)
      Hamamatsu R2083

      		0.7ns
      		 0.37ns (FWHM)
      Hamamatsu R9779

      		1.8ns
      		 0.25ns (FWHM)
      Hamamatsu R9800

      		1.0ns
      		 0.27ns (FWHM)

    4. Using Hamamatsu R9779 timing specifications: TTS 250ps, rising time 1.8ns, QE 15%
  3. Original photon yield: assuming scintillator efficiency of 0.003 (fraction of energy converted to UV and visible photons) or 1E3 photon/1MeV assuming 3eV/photon. This was deduced from :
    1. An earlier CLAS TOF test (nucl-ex/0506020) which claimed a MIP yield of 685+/- photoelectrons/4.4MeV, divided by 15% of QE and multiplied by (3eV) of average photon energy.
    2. Our Preshower yield (however the preshower is a different scintillator) showed roughly 4E-3 of energy conversion.
    3. Some online searching, for example Table 1 in http://iopscience.iop.org/0295-5075/95/2/22001/pdf/epl_95_2_22001.pdf, showed BC408 with 10000 photon/MeV. This is 10 times higher. However there is no original reference from Saint-Gobain to prove this.
  4. Procedure:
    1. Calculate nominal number of photons nph0 using 2 MeV/g/cm^2 and the scintillator thickness;
    2. Simulate 400 events. For each event, use Gaussian distribution to simulate the number of photons with mean nph0 and sigma=sqrt(nph0). However, due to the large nph0 used (even for 0.5cm thickness), delta-t was observed to increase only slightly compare to fixed nph=nph0.
    3. loop over all photons, following uniform solid angle distribution, surface reflection assuming 0.99 for total internal reflection (1% loss) and 0.95 otherwise (5% loss, Tyvek wrapping), for attenuation using half with the first attenuation length and half with the bulk attenuation length, calculate probability.
    4. Do the following for photons reaching left and right edges separately:
      1. When the photon reaches the readout edge, decide whether it is a successful photon by (random#)<(QE*probability)? -- note that to save CPU time can also reduce the total number of photons nph by QE, and here use only (random#)<probability.
      2. For successful photons, calculate the time needed to reach the readout edge, add in PMT's TTS to get the signal start time. Then, simulate the signal using a triangular pulse with rise time = (PMT rise+scintillator rise), and assuming equal rise and fall times;
      3. Summing all photons together, generate signal vs. time, calculate rise time (10%-90% of maximum->t1,t2; rise time=t2-t1), pulse arrival time (t1+t2)/2, and the standard deviation of the arrival time (delta-t).
    5. For detector with both edges readout, calculate spread in (t_left+t_right)/2 as the timing resolution, and photoelectron left+right as the total yield.
    6. If applicable, loop over 10 thicknesses from 0.5 to 5.0cm, also loop over 20 x values (position from left to right, or from inner to outer edge for SPD) to study the position dependence. Position uncertainty can be added here using uniform random distribution from -delx to +delx.
  5. Comparison of simulation (1000 events) with known data: (brief info on CLAS12 FTOF can be found here.)
    		Simulation
    		PMT (TTS), TDC (resolution) used
    		 Comment
    Detector and size in cm
    		 Data and Ref # ph.e. (center-edge)
    		 delta-t (c-e)

    HRS S2 40(w)x60(L)x0.5(th)
    		 300ps (Hall A NIM)
    		 34-70
    		 295-310ps
    		 Burle 8575 (2.0ns sigma, QE=25%), LeCroy 1875 (100ps)
    		 dominated by PMT TTS due to low nphe; PMT QE from Doug' catalog page
    HRS S2m 14(w)x43(l)x5(th)
    		 100ps (S2m study?), 200ps for transversity coincidence timing, light yield about 600 (Bogdan).
    		 425-510
    		 53ps
    		 XP2282B (0.4ns sigma), LeCroy 1875 (50ps)
    		 used light guide 0.7 efficiency to get close to 600 ph.e.; delta-t dominated by TDC
    CLAS12 TOF test 6(w)x69(l)x6(th)
    		 34ps (USC note)
    		 650-1000
    		 36-39ps
    		 R9779 (0.25ns FWHM); V1290N pipeline TDC (32.5ps) -- these are USC test conditions
    		 dominated by TDC
    CLAS12 TOF test 6(w)x203(l)x6(th)
    		 51-58ps (USC note)
    		 230-750
    		 52-81ps
    		 PMT TTS starts to contribute for edge events.
    CLAS panel-1A TOF counter 15(w)x213(l)x5(th), BC408
    		 138 ps (USC note); 118ps (1999, used XP2262)
    		 147-335
    		 72-100ps
    		 don't understand why can't get USC data

    1. For SPD, assuming rectangular shape with width the average of inner and outer edges. FASPD: 4.1cm x 132cm (instead of the trapezoid shape: sketch); LASPD: 11.15cm x 57cm (trapezoid sketch). Light is directly coupled to a PMT attached to one edge. The results are shown below.
      1. As a reminder, we would like
        1. delta-t<100ps;
        2. number of photoelectrons >10 (original SPD estimate, requiring preamp gain 20), >40 would allow us to use existing PMT pre-amp with gain~5;
        3. signal arrival time is relevant for online coincidence timing (no position info);
        4. pulse rise time is required to <2.0ns.
        5. For SoLID offline analysis we use position from GEM, need to add that position resolution on top of the results below. But that uncertainty should be quite negligible if delta-x is at mm level.
        6. The simulation used 60ps of TDC resolution (ref: Alexandre C.)
        7. The simulation assumed R9779. Comparison between R9779, R9800, and fine-mesh PMT is as follows:
          PMT
          		 R9779
          		 R9800
          		 R5505-70 (fine-mesh, low gain)
          		 R5924-70 (fine-mesh)
          		 R7761-70 (fine-mesh)
          		XP2262
          rise time (ns)
          		 1.8
          		 1.0
          		 1.5
          		 2.5
          		 2.1
          		2.3
          transite time (ns)
          		 20
          		 11
          		 5.6
          		 9.5
          		 7.5
          		31
          transit time spread TTS (ns)
          		 0.25 (FWHM) 0.27 (FWHM) 0.35 (FWHM)

          		0.7 edge-center, 0.5 (??)
          diameter
          		 51mm
          		 25mm
          		 25mm
          		 51mm
          		 38mm
          		51mm
          effective area
          		 46mm dia or 16.62 sq.cm
          		 22mm dia or 3.80 sq.cm
          		 17.5mm dia or 2.41 sq.cm
          		 39mm dia or 11.95 sq.cm
          		 27mm dia or 5.73 sq.cm
          Typical gain

          		5E5 at 0T; 2E4 at 1T (at 0 deg, less with an angle)
          		 1E7
          		 1E7

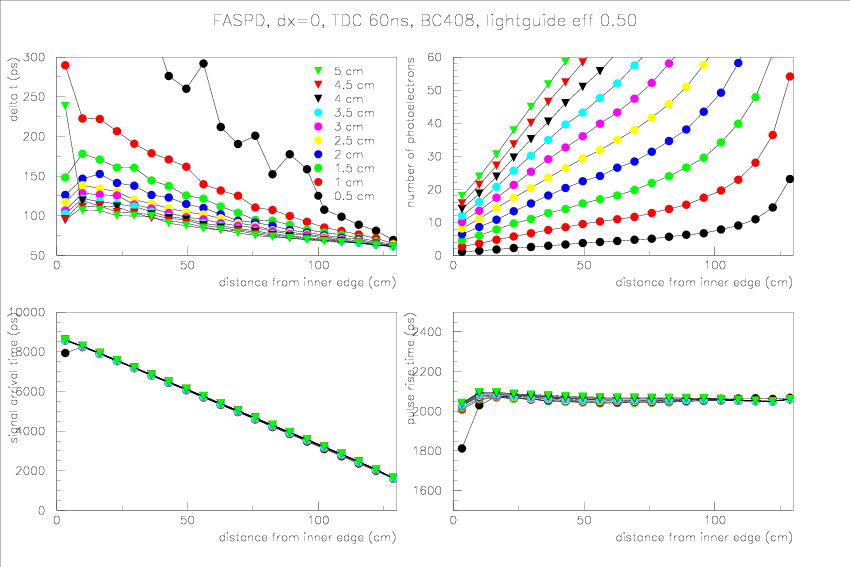
      2. FASPD, without position uncertainty, TDC resolution 60ns, light guide efficiency 50%, BC408FASPD with delx=0
      3. LASPD, without position uncertainty, TDC resolution 60ns, light guide efficiency 50%, BC408
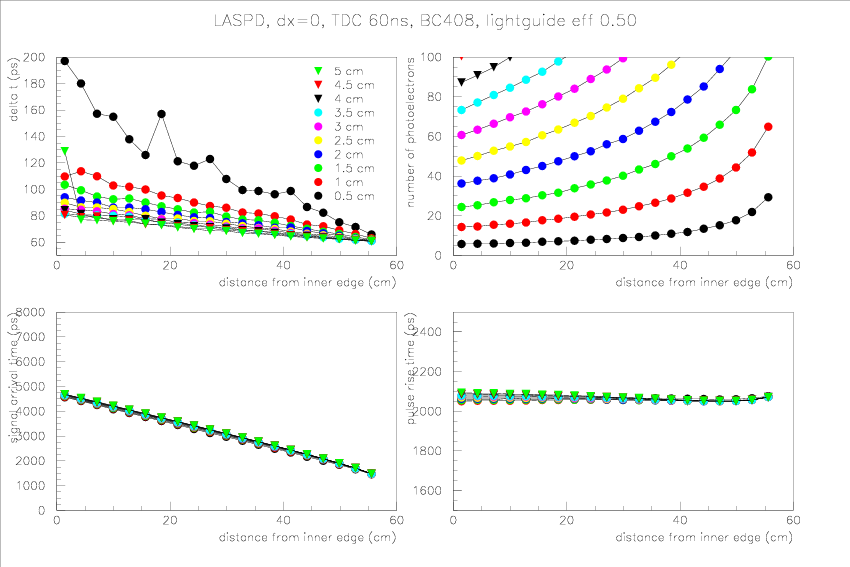
      4. LASPD with delx=0
    2. Conclusion:
      1. numbre of photoelectrons is important. Large nphe minimize all contributions to the timing spread (except for the finite position uncertainty). This indicates the use of clear fibers (with trapping efficiency no larger than 10%) is impossible.
      2. Use of good PMT (small TTS) and TDC (small resolution) is important, since for high light yield these two factors dominate the timing resolution. It's also crucial we test all PMTs before using, since CLAS experience is that the PMT spec may be 2-3 times worse than the manufacturer's values.
      3. For LASPD, 1cm-2cm might be okay.  Depending on photon rej performance, the thicker the safer for timing resolution.
      4. Light yield for FASPD is a problem for inner edge, mostly due to the length of the SPD. Based on this, for FASPD we will need to go back to the scintillator+WLS fiber and the 4 radial+60 azimuthal segmentation design. Here is a sketch based on equal-ratio segmentation in the radial direction.
      5. Prototype testing is important to pin down light output and timing.
    3. Simulation for SDU square tiles -- for calibrating the light output, use XP2262 directly coupling to one side. For 5mm and thicker tiles, data are consistently higher than simulation. However, simulatio for USC CLAS12 TOF pads and HRS S2 agree well with data.  This indicates the scintillator conversion is about 0.01 (not 0.003), but the light guides reduce the output. The 3mm result indicates something other than light conversion is coming into play for very thin tiles.
      SDU tile size
      		 light output, simulated
      		 light output, measured
      10x10x0.3
      		 10 p.e.
      		 8.2 p.e.
      10x10x0.5
      		 20 p.e.
      		 48.1 p.e.
      10x10x1.0
      		 47 p.e.
      10x10x2.0
      		 106 p.e.