An Introduction to Thermoelectrics
©2001 Tellurex Corporation
1248 Hastings
Traverse City, Michigan 49686 (231)947-0110

A Brief History

Early 19th century scientists, Thomas Seebeck and Jean Peltier, first discovered the phenomena that are the basis for today's thermoelectric industry. Seebeck found that if you placed a temperature gradient across the junctions of two dissimilar conductors, electrical current would flow. Peltier, on the other hand, learned that passing current through two dissimilar electrical conductors, caused heat to be either emitted or absorbed at the junction of the materials. It was only after mid-20th Century advancements in semiconductor technology, however, that practical applications for thermoelectric devices became feasible. With modern techniques, we can now produce thermoelectric “modules” that deliver efficient solid state heat-pumping for both cooling and heating; many of these units can also be used to generate DC power in special circumstances (e.g., conversion of waste heat). New and often elegant uses for thermoelectrics continue to be developed each day.

A Closer Look

A typical thermoelectric module consists of an array of Bismuth Telluride semiconductor pellets that have been “doped” so that one type of charge carrier– either positive or negative– carries the majority of current. The pairs of P/N pellets are configured so that they are connected electrically in series, but thermally in parallel. Metalized ceramic substrates provide the platform for the pellets and the small conductive tabs that connect them. The pellets, tabs and substrates thus form a layered configuration. Module size varies from less than 0.25" by 0.25" to approximately 2.0" by 2.0". Thermoelectric modules can function singularly or in groups with either series, parallel, or series/parallel electrical connections. Some applications use stacked multi-stage modules.


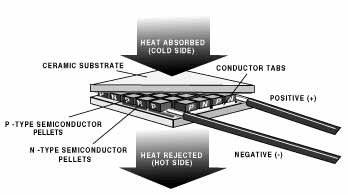
Cooling, Heating: When DC voltage is applied to the module, the positive and negative charge carriers in the pellet array absorb heat energy from one substrate surface and release it to the substrate at the opposite side. The surface where heat energy is absorbed becomes cold; the opposite surface where heat energy is released, becomes hot. Using this simple approach to “heat pumping”, thermoelectric technology is applied to many widely-varied applications– small laser diode coolers, portable refrigerators, scientific thermal conditioning, liquid coolers, and beyond.

Power Generation: Employing the effect which Seebeck observed, thermoelectric power generators convert heat energy to electricity. When a temperature gradient is created across the thermoelectric device, a DC voltage develops across the terminals. When a load is properly connected, electrical current flows. Typical applications for this technology include providing power for remote telecommunication, navigation, and petroleum installations.

A Comparison of Cooling Technologies

The flow of heat with the charge carriers in a thermoelectric device, is very similar to the way that compressed refrigerant transfers heat in a mechanical system. The circulating fluids in the compressor system carry heat from the thermal load to the evaporator where the heat can be dissipated. With TE technology, on the other hand, the circulating direct current carries heat from the thermal load to some type of heat sink which can effectively discharge the heat into the outside environment.


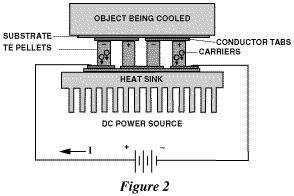
Each individual thermoelectric system design will have a unique capacity for pumping heat (in Watts or BTU/hour) and this will be influenced by many factors. The most important variables are ambient temperature, physical & electrical characteristics of the thermoelectric module(s) employed, and efficiency of the heat dissipation system (i.e., sink). Typical thermoelectric applications will pump heat loads ranging from several milliwatts to hundreds of watts.

Thermoelectric Benefits

The choice of a cooling technology will depend heavily on the unique requirements of any given application, however, thermoelectric (TE) coolers offer several distinct advantages over other technologies:

• TE coolers have no moving parts and, therefore, need substantially less maintenance.

• Life-testing has shown the capability of TE devices to exceed 100,000 hrs. of steady state operation.

• TE coolers contain no chlorofluorocarbons or other materials which may require periodic replenishment.

• Temperature control to within fractions of a degree can be maintained using TE devices and the appropriate support circuitry.

• TE coolers function in environments that are too severe, too sensitive, or too small for conventional refrigeration.

• TE coolers are not position-dependent.

• The direction of heat pumping in a TE system is fully reversible. Changing the polarity of the DC power supply causes heat to be pumped in the opposite direction– a cooler can then become a heater!

Design Calculation Tutorial

Let's assume a solid-state electronic component requires cooling to improve performance and reliability. The component resides in an environment with a maximum ambient air temperature of 50°C and dissipates 15 Watts. Cooling the component to 25°C will improve performance and reliability.

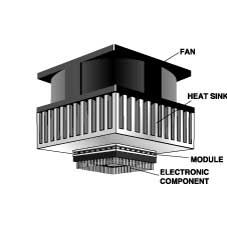
Our thermoelectric cooling system will have the following physical characteristics:
the electronic component will be in direct contact with cold side of the TE cooler, and the heat sink and fan will be in direct contact with hot side of the TE cooler.

The natural flow of heat is always from hot to cold. When DC power is applied to the thermoelectric module, the cold side becomes colder than the electronic component, so heat flows naturally from the component to the TE module.

The charge carriers in the semiconductor material relocate the heat from the electronic component to the heat sink. This causes the temperature of the heat sink to rise. When the temperature of the heat sink exceeds that of the surrounding air, heat will flow naturally from the sink to the atmosphere.

System Design

Our known design values are:

Q = 15 Watt heat load from electronic component

TA = 50°C maximum ambient air temperature

TC = 25°C required temperature of electronic component

Prior to using the performance graphs to determine which TE cooler is appropriate for our application, we must first identify the hot side temperature (TH) and the resultant temperature differential across the module (ΔT).

The hot side temperature will be equal to the ambient temperature (TA) plus the rise in temperature across the heat sink from dissipating the heat load (Q) and the TE module power (V x I).

TH = TA + (V x I + Q) RQ

where RQ = thermal resistance of heat sink in C° temperature rise per Watt dissipated. In this design, we will keep the rise of the heat sink temperature to no more than about 15°C above ambient. This would give us a TE module hot side temperature of about 65°C.

TH = 50°C + 15°C = 65°C

The temperature differential across the module can now be calculated as follows:

ΔT = TH - Tc = 65C - 25C = 40C

Module selection: The performance graphs for each of the modules provide data for four different TH conditions. The X axis along the lower part of the graphs lists potential ΔT in C°. The Y axis at each side of the lower graphs lists potential heat load in Watts. The diagonal lines in the lower part of the graph identify the Q vs ΔT ratio for several arbitrarily selected currents: I = 2.7A, 3.1A, 3.5A and IMAX 3.9A.



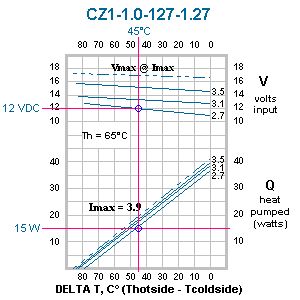
Let's consider using a CZ1-1.0-127-1.27 Z-Max® module. First locate the graph for TH = 65°C [Fig. 4]. Then locate the heat load Q = 15W . Sight along a horizontal line to the point that intersects with the diagonal line I = 2.7A. Sight down to determine ΔT = 45°C. This is 5°C greater than the requirement and provides a margin of safety for variation in assembly.

We can now determine the voltage requirement by extending the vertical DT = 45°C line to the upper part of the graph. At the intersection of I = 2.7A, extend a horizontal line to the side of the graph where voltage input is listed. The voltage requirement is 12VDC.

Heat sink selection: The values identified in the preceding first pass analysis are used to assess overall system feasibility. We want to qualify our assumption of 15°C rise across heat sink.

The heat pumping capability of the thermoelectric module is significantly influenced by the efficiency of the heat sink. The hot side of the module must interface with an efficient heat removal system to achieve useful temperature differential across the module.

Natural convection, forced convection, and liquid cooled are three of the most common types of heat sinks. Thermal resistance varies among the different types and sizes of sinks with natural convection being the least efficient and liquid cooled the most efficient. The majority of thermoelectric cooling applications use forced convection heat sinks with thermal resistance values (RQ) ranging from 0.10°/W to 0.5°/W.

Using values now known for TA V, I, and Q we can solve for RQ to determine if it is reasonable:

RQ = (TH - TA)/(V x I +Q)=(65°C - 50°C)/(12V x 2.7I +15W)
RQ = 0.32°C/W

Our proposed system using a CZ1-1.0-127-1.27 Z-Max® module and a forced convection sink/fan combination meets or exceeds the criteria for this application.

Power Supply: Typical power sources for thermoelectric coolers include batteries, automotive and marine DC systems, AC/DC converters, and linear and switched DC power supplies.

The Thermoelectric “Sweet Spot”



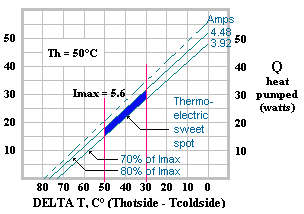
Ninety per cent of all practical applications for thermoelectric technology fall within a very narrow range of operating conditions.

1. Temperature differential (Delta T) between 30°C and 50°C

2. Thermoelectric module current draw (l) between 70% and 80% of IMAX, and

3. Co-efficient of performance (COP) between 0.25 and 0.4.

Passive Load

In designing a thermoelectric (TE) system, one of the most important processes, is reaching an understanding of your thermal load. Without this vital information, you cannot wisely choose the best TE device or heat exchangers for the job. Each thermoelectric system has a unique capacity for moving heat. While it is possible to simply build up a system and then see what it will do, it is usually far more prudent to optimize your system for the desired outcomes. There is no better place to start, than with a good, solid estimate of how much heat must be removed from your thermal load to achieve the performance objectives.

There are two components to thermal load in TE systems: active and passive. Active load is found whenever part of the load actually produces heat. An example would be an electronic circuit in an enclosure; the circuitry would dissipate wattage based on its voltage and current requirements. Many TE applications don’t have an active load (e.g., a food and beverage cooler) and this term can be entirely discounted in these cases. Nearly all TE systems, however, must cope with the passive portion. To maintain a temperature difference between a thermal load and the ambient environment, a certain amount of energy must be continually moved into (for heating) or out of (for cooling) the load. The rate at which this energy is moved (usually expressed in watts), is the passive load.

One way to conceptualize passive load, is to look at it like a leaky boat. Water is continually streaming into the boat through all of the various leaks (e.g., holes, faulty seals, etc.). The more leakage there is, the faster the water will come into the boat. Faced with this situation, if you wanted to maintain the boat at a certain level in the water (and you couldn’t repair the leaks), you would have to bale out the water at a certain rate. If you bale too slowly, the boat will sink lower; if you dump the water too quickly, you may rise above the desired level (which may or may not be a problem). Ideally, of course, you would repair the boat at the first opportunity so you could minimize your future rate of baling.

With a TE system, you are trying to keep your thermal load colder or hotter than the ambient temperature. Unfortunately, no matter how well you design your system, there will be some leaks. There is no type of insulation with an infinite thermal resistance, so some heat will pass right through your primary line of defense. Furthermore, seals used to cope with the inevitable holes (e.g., doors, TE engine pass-through, etc.), will also be imperfect. Thus, in a cooling application, some heat is going to leak into the thermal load from the ambient environment. To paraphrase a popular sports expression, “You can’t stop it, you can only try to contain it”. So you bale, only this time you are baling out heat, and you’re not using a bucket or a water pump, but a thermoelectric system—one which is steadily pumping watts out of (or into for heating) the thermal load.

So . . . how do you quantify your passive load? First you have to identify the greatest temperature difference (between your thermal load and the ambient environment) that can occur. For instance, if you’re cooling, what is the highest ambient temperature and how cold will your load need to be in that circumstance. This is generally your worst case. If you design your system so that you’ll have enough cooling capacity in that worst case, you’ll have more than enough potential for every other situation. The worst-case difference between your ambient and load temperatures, will be your 'Delta T' in the equations which follow.

The Nature of Passive Load

The transfer of heat from a load to the ambient environment, is largely a function of two thermal processes—conduction and convection. Conduction is the transfer of heat through matter (insulation, structural components, seals, fasteners, etc.) and is a function of the temperature difference (i.e., Delta T) across the material, the physical dimensions, and the thermal conductivity of the material (K). Convection is heat transfer across the boundary layer of air at the surface of a material. It is a function of the Delta T across the boundary layer and the rate of air movement at the surface—the faster the air movement, the greater the convection of heat.

With a well-insulated thermal load (e.g., an insulated enclosure), convection is a relatively inconsequential component and you can often focus exclusively on the conductive element. The following equation can be used to estimate a purely conductive load:



where

Q
is the amount of heat conducted (it can be expressed in either BTU/hour or watts, although in the thermoelectric industry, most support documentation is based on wattage);
ΔT
is the temperature difference between the thermal load and the ambient environment (in F° for BTU/hour calculations, in C° for watts);
K
(Kappa) is the thermal conductivity of the material expressed in either BTU/hour-feet-F° or watts/meter-C°;
L
is the thickness of the material (in feet for BTU/hour calculations, meters for watts); and
A
is the exposed surface area of the material (in square feet for BTU/hour calculations, square meters for watts).

If you want to include both the conductive and convective components of the load, you can use this equation:



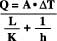
where

Q
is the amount of heat conducted and convected (expressed in either BTU/hour or watts);
K
(Kappa) is the thermal conductivity of the material expressed in either BTU/hour-feet-F° or watts/meter-C°;
h
is the heat transfer coefficient (in still air, this ranges between 4-5 BTU/hour-feet2-F° or 23-28 watts/meter2-C°; in turbulent air, h falls in the range of 14-20 BTU/hour-feet2-F° or 85-113 watts/meter2-C°);
L
s the thickness of the material (in feet for BTU/hour calculations, meters for watts);
A
is the exposed surface area of the material (in square feet for BTU/hour calculations, square meters for watts); and
ΔT
is the temperature difference between the thermal load and the ambient environment (in F° for BTU/hour calculations, in C° for watts).

Note that the result that you get for Q with this equation will be lower than that obtained for the formula based only upon conduction. This is because the convection/conduction equation accounts for two sources of thermal resistance to heat flow. With the calculation reflecting a slightly greater series resistance to heat leakage, it logically follows that fewer watts will be indicated to compensate for passive load.

When you are dealing with an uninsulated load, or an uninsulated portion of one (e.g., a cold plate), then it becomes very important to explore the convective part of thermal load. In these situations, convection may offer the primary resistance to the leakage of heat. Remember that in some situations (e.g., an uninsulated enclosure), you will have air movement on both the inside and outside; as a result, your Delta T will be split between the two boundary layers (based on the relative convectivity of each). As you will find in using the equation below to estimate your convective load, without insulation, you will need to pump a lot more wattage with your TE system.



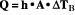
where

Q
is the amount of heat convected (expressed in either BTU/hour or watts);
h
is the heat transfer coefficient (in still air, this ranges between 4-5 BTU/hour-feet2-F° or 23-28 watts/meter2-C°; in turbulent air, h
falls in the range of 14-20 BTU/hour-feet2-F° or 85-113 watts/meter2-C°);
A
is the exposed surface area of the material (in square feet for BTU/hour calculations, square meters for watts); and
ΔTB
is the temperature difference across the boundary layer at any exposed surfaces (in F° for BTU/hour calculations, in C° for watts).

When dealing with enclosures, you can also estimate your passive load empirically once a prototype is built. Simply place a known heat load inside (make sure that the enclosure can 'take the heat'), then monitor the temperatures of the ambient and enclosure interior. Once the Delta T between the inside and ambient has stabilized, you can use the following equation to determine the passive load:



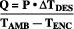
where

Q
is the passive load, expressed in watts;
TAMB
is the ambient temperature after stabilization (in C°);
TENC
is the enclosure temperature after stabilization (in C°);
ΔTDES
is the desired temperature difference between the inside of the enclosure and the ambient environment (in C°); and
P
is the power dissipation within the heater employed for the test (expressed in watts).


System Assembly

Several methods for installing thermoelectric modules have been developed, including: mechanical clamping, epoxy bonding, and direct solder bonding. The individual requirements of the application will determine which method is most appropriate, however, mechanical clamping is by far the most common.

Thermoelectric modules are relatively strong in compression and weak in shear
Whichever method of installation is used, it is important to avoid excessive mechanical loading of the module.

Thermal resistance occurs at each interface of an assembly and affects overall system performance. In mechanically-clamped systems, the recommended flatness of interface surfaces should be within 0.001". Even with this degree of flatness, interface materials must be used to fill in the small thermal gaps; typical choices include silicone-based thermal grease, graphite foil, and thermally-conductive pads.
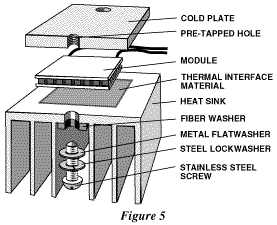
Special care must be taken to insure that uniform pressure is applied during installation. Recommended procedures for mechanical clamping are illustrated in Figure 5.

Mechanical Clamping Method

The following is a list of guidelines for using mechanical clamping:

1. The mounting surfaces (between which modules are to be clamped) should be flat to within 0.001".

2. Mounting and module surfaces should be carefully cleaned to remove any grit, burrs, etc.

3. If more than one module is to be used in the assembly, all modules should be within 0.001" in height.

4. Coat the hot side of the module with a thin layer of thermal grease, then place it on the heat sink. Applying firm but even downward pressure, move the module in clockwise/counter clockwise motions. Do this until a slight resistance is felt and excess thermal grease is squeezed out.

5. Coat the cold side of the module with a thin film of thermal grease. Repeat the process described in step 4.

6. Bolt the object to be cooled and heat sink together using stainless steel fasteners with washers or split type lockwashers. Insure an even pressure across the module surface when tightening the screws. Maximum recommended compression loading is 350 lbs. per sq. inch of module surface. ©2001 Tellurex Corporation