Position Resolution Study
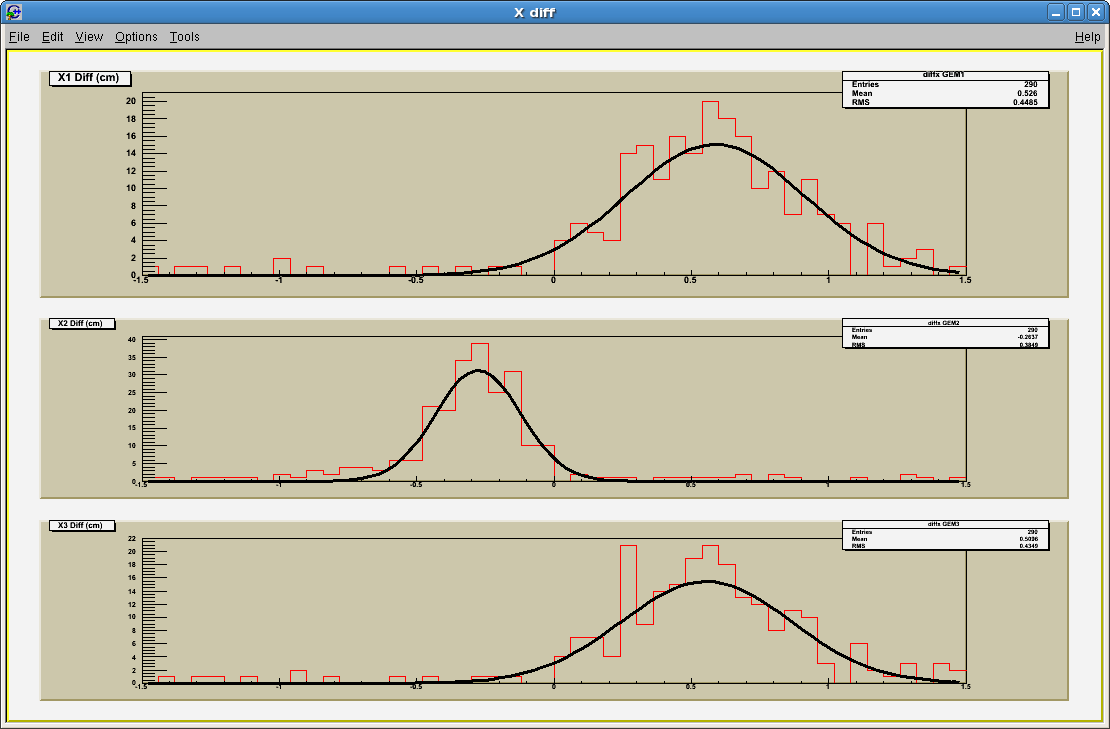
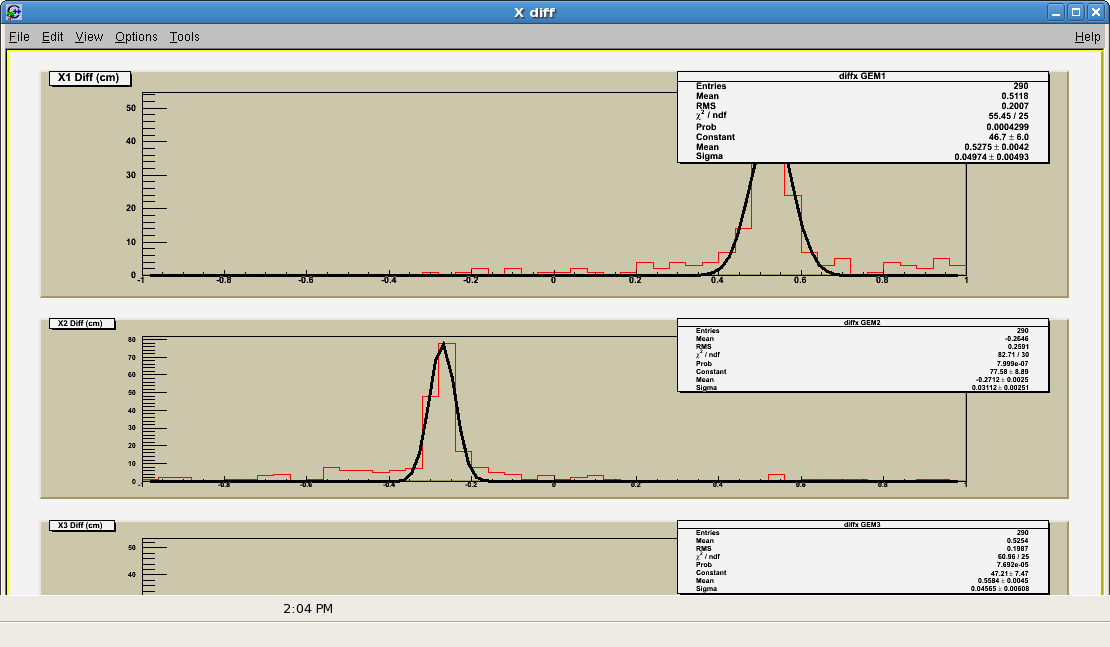
Before we made any corrections to it, a count of the difference between measured path and predicted path using the other 2 gems
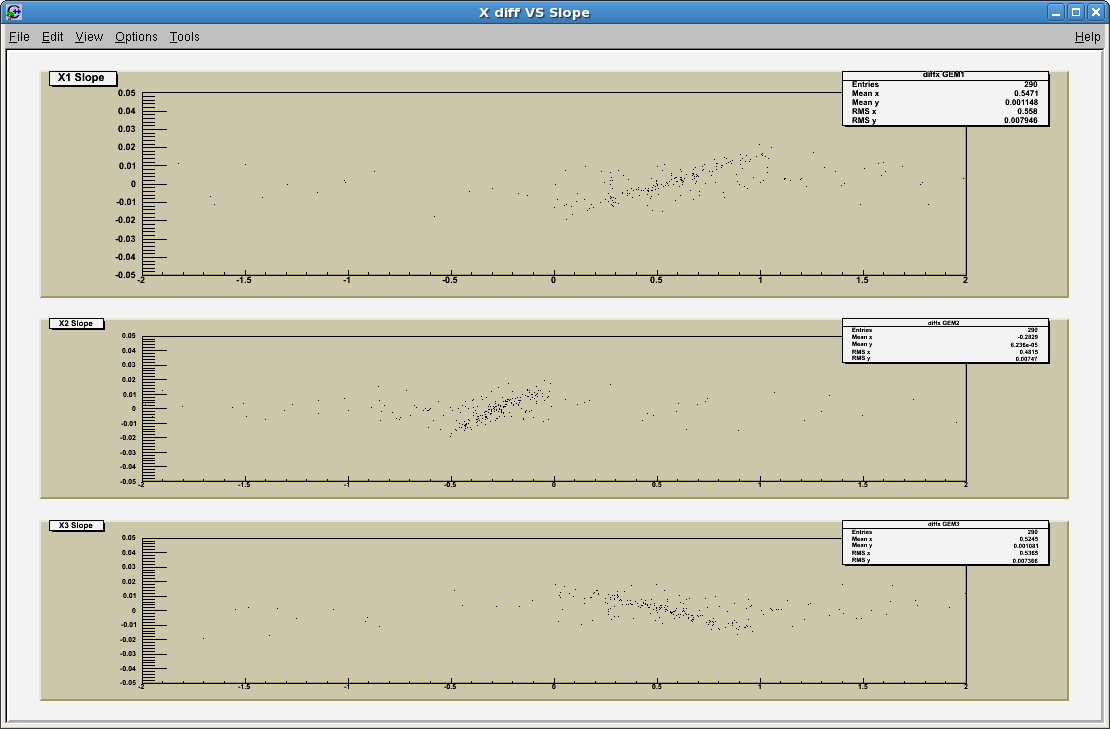
Using a slope vs difference plot, we noticed a correlation that should not have been there.
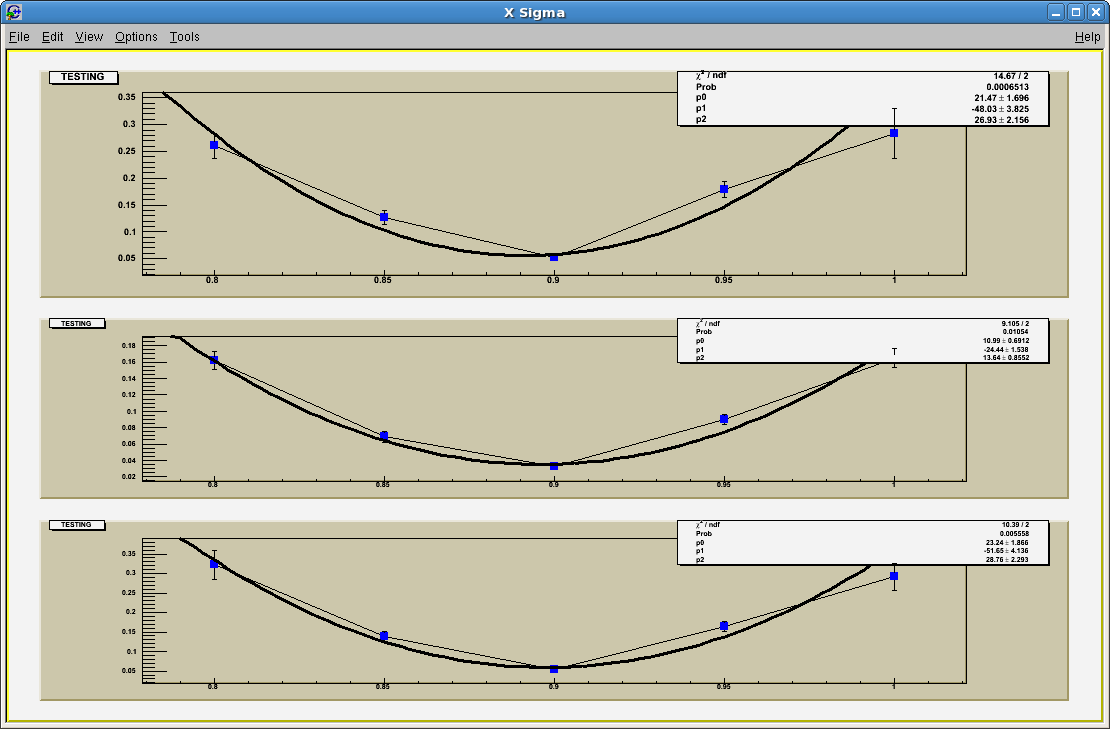
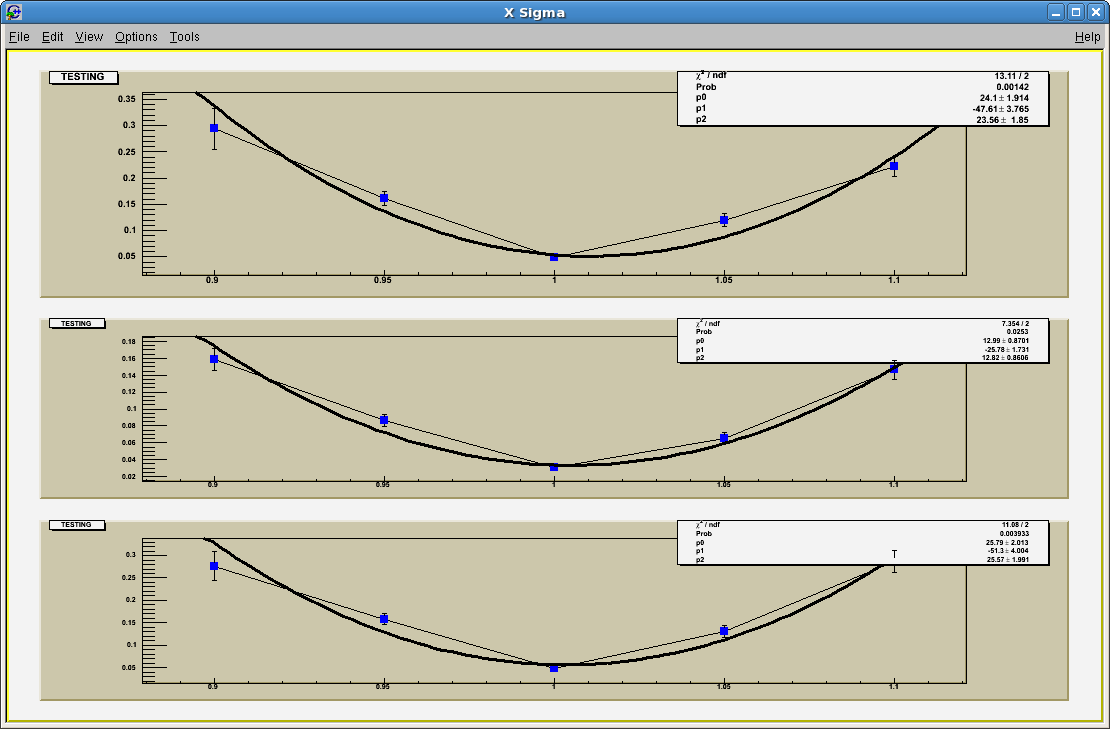
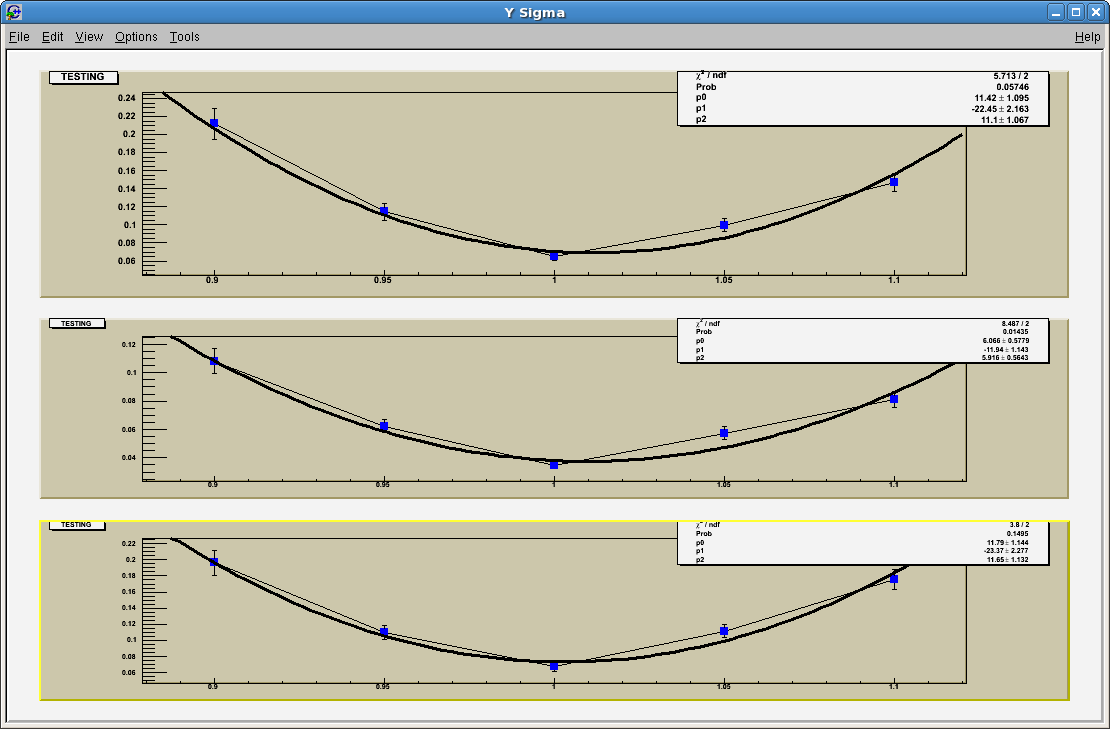
We decided that our Z distance (distance between gems) was off. This could have been due to human error or not know where exactly a partical interacts with the gas. Using RMS VS %Z distance we got the following.
Using the parameters, we can concluded what the lowest Sigma was and adjusted the the Z distance. Our final difference looked like this.
The goal is to figure out what the error on the gems is. 75um is the assumed error, but we wanted to calculate it using our data.
With a Gaussian error distribution we must use <math>\Delta x_d^2 = \Delta x_1^2 + \Delta x_2^2</math>. using this we can calculate the error.
The final equations for the error come out to be: <math>\Delta x_1 = \Delta x1_D/3.23</math>, <math>\Delta x_2 = \Delta x2_D/1.57</math>, <math>\Delta x_3 = \Delta x3_D/3.23</math>.
GEM1
X: 153.99μm
Y: 203.90μm
GEM2
X: 198.22μm
Y: 216.88μm
GEM3
X: 141.33μm
Y: 186.35μm