Plan for Diffusion Parameter

Right now, our largest uncertainty in the polarization comes from the diffusion of the polarization. We have calibrated our NMR signal to the polarization in the pumping chamber of the cell. The NMR signal is measured in the lower chamber. As $3$He gas flows from one chamber to the other, it is no longer in contact with the polarized alkali metal, and starts to depolarize. We can think of a polarization current that flows from one chamber to the other.

$$J(z)=\frac{1}{2}n(z)D(z) \frac{dP}{dz}$$ (1)

Where $n(z)$ is the density of helium and $D(z)$ is the diffusion coefficient. Both are functions of position along the transfer tube due to the thermal gradient. After conserving the current and integrating along the transfer tube, we get

$$J=\frac{1}{2}D_t\frac{n_t}{L}K\left(P_p-P_t\right)$$ (2)

K is a constant that depends on the ratio of temperatures in the target and pumping chambers.

The rate of change in polarization due solely to diffusion (for each chamber) is therefore

$$\frac{dP_p}{dt} = -\frac{2J A_{tr}}{n_p V_p}$$ (3)

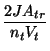$$\frac{dP_t}{dt} = \frac{2J A_{tr}}{n_t V_t}$$ (4)

Finally, we are left with the following for the change in polarization due to diffusion.

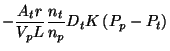$$\frac{dP_p}{dt} = -\frac{A_tr}{V_p L}\frac{n_t}{n_p} D_t K \left(P_p-P_t\right)$$ (5)

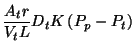$$\frac{dP_t}{dt} = \frac{A_tr}{V_t L} D_t K \left(P_p-P_t\right)$$ (6)

This almost completely describes the polarization in the target chamber, since the polarized gas can only come from the upper chamber. The gas in the upper chamber, however, is continually polarized. The change in polarization in the upper chamber is

$$\frac{dP_p}{dt} = -\frac{A_tr}{V_p L}\frac{n_t}{n_p} D_t K \... ...- \left(\gamma_{SE}^{Rb} + \gamma_{SE}^K + \Gamma_p P_p\right)$$ (7)

The target chamber polarization only needs a correction due to the depolarization effects in the target chamber.

$$\frac{dP_t}{dt} = \frac{A_tr}{V_t L} D_t K \left(P_p-P_t\right) - \Gamma_tP_t$$ (8)

If we consider $P_t^{\infty}$ and $P_p^{\infty}$, the equilibrium cases, then we can set equations 7 and 8 equal to zero and conserving the number of particles in the cell, we can finally write the equalibrium polarization of the target chamber in terms of the pumping chamber.

$$P_t^{\infty} = \frac{P_p^{\infty}}{1+\frac{\Gamma_t}{D_t}}$$ (9)

In priciple this equation has everything that we need to determine the relationship between the two chambers. In reality, we need to take this a step or two further. When the beam is on (or has recently been on, as is the case for most of our EPR calibrations), we need to determine the effect of the beam on the polarization.

$$\Gamma_t^{beam ON} = \Gamma_t^{beam OFF} + \Gamma_{beam}$$ (10)

We do not have a direct measurement of $\Gamma_t^{beam OFF}$ for our in-hall setup. However, it can be approximated at a very high level from the data taken at UVa.

We have NMR signals at times where the beam was on and the beam was off. This will allow us to extract the polarization. Another way to write the polarization in the chambers makes this clear:

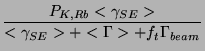$$P_{p,t}^{Beam ON} = \frac{P_{K,Rb}<\gamma_{SE}>}{<\gamma_{SE}>+<\Gamma>+f_t\Gamma_{beam}}$$ (11)

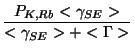$$P_{p,t}^{Beam OFF} = \frac{P_{K,Rb}<\gamma_{SE}>}{<\gamma_{SE}>+<\Gamma>}$$ (12)

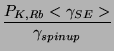$$= \frac{P_{K,Rb}<\gamma_{SE}>}{\gamma_{spin up}}$$ (13)

Where $f_t$ is the fraction of particles in the target chamber, $\Gamma_{beam}$ and $\gamma_{spin up}$ is the inverse of the time constant measured for the cell.

Since we are measuring in the same chamber without moving the cell at all, we can take a ratio of the signals, and let the factors of flux and calibration constant cancel

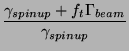$$\frac{S^{beam ON}}{S^{beam OFF}} = \frac{P_t^{beam ON}}{P_t^{beam OFF}} = \frac{\gamma_{spin up} + f_t\Gamma_{beam}}{\gamma_{spin up}}$$ (14)

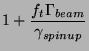$$= 1+\frac{f_t\Gamma_{beam}}{\gamma_{spin up}}$$ (15)

I have already determined $\gamma_{spin up}$.

$$1/\gamma_{spin up} = 6.174 \pm 0.058 h$$

. I am working on establishing a good ratio for $P_t^{beam ON}/P_t^{beam OFF}$. Once this is accomplished, I will be able to use equation 9 to determine the polarization in the lower chamber.